[Quant 전략] 변동성 조정 포트폴리오 (Volatility Managed Portfolio 전략

 

I. Conditional Volatility Targeting 전략 (Bongaerts et al.)

 

논문 출처 : The Performance of Volatility-Managed Portfolios

 

1) 평상시 (unscaled risk exposure, I = 0)

2) 변동성 국면 (scaled risk exposure, I = 1)

 

• T-1 시점까지의 매월 변동성을 계산 (일간 수익률 기준)
• T-1월까지의 변동성 데이터를 5분위로 나눠서 T-1 시점의 변동성이 1분위(가장 높은 분위)에 해당하면 high volatility, 5분위에 해당하면 low volaitility, 2~4분위에 해당하면 medium volaitility
• 변동성이 낮은 국면에서는 레버리지 / 변동성이 높은 국면에서는 편입비를 낮추는 효과
• 타겟 변동성 : 현재까지의 모든 일간 수익률 데이터로 계산한 변동성 값을 사용
• 최대 레버리지 비율 : 가용 최대 익스포저

 

II. 이걸 응용해보려고 하면 두 가지 정도의 문제점이 발생

 

1. 매일 어제까지의 일간 수익률 데이터로 어제 하루 동안 (일중 데이터를 구하는게 가능하다면) 아니면 최근 1주 혹은 2주 등 짧은 기간 동안의 변동성이 전체 데이터 중 몇 분위에 해당하는지 확인..

→ 일중 수익률이 있어야 가능할 것으로 보임

 

2. 일간 수익률을 이용해서 매월 익스포저를 결정하는건 너무 대응이 느림. 변동성 군집현상이 한달 안에 사라질 수도 있기때문에 T-1 월의 변동성이 T월로 이어지지 않을 수 있음. 그러면 예를 들어, 3월에 급락으로 높은 변동성이 계산되었는데 4월에는 완만한 회복장세를 보이는 경우, 3월에 높은 변동성을 보고 4월 포지션을 작게 가져갔다가 4월의 시장 상승분을 따라가지 못하는 현상 발생할 수 있음

분홍색 : 과거 데이터 기반 매월 변동성의 분위 수 / 파란색 : 실제 월간 변동성

 

III. 그럼 어떻게 해결?

 

최근 N일 동안의 rolling 변동성 계산한 후 과거 시점에서 계산된 rolling 변동성들의 분포 중 몇 분위에 해당하는지 계산

→ 이 방법 또한 최근 급락 구간에 변동성이 커지면서 일종의 쫄보(?)가 되는 효과가 나타나서 급락 이후 이어지는 급등 구간의 시장을 따라갈 수 없게 됨 (뒤에 결과에서 다시 확인)

분홍색 : 과거 30일 변동성의 분위 수 / 파란색 : 실제 직전 30일 변동성

 

IV. 분석 결과

 

< Parameters >

• 변동성 구간 계산 : 20일
• 고변동성 구간에서의 최소 레버리지 비율 : 60% (주식-파생형 펀드 기준 주식 최소 편입비 가정)
• 저변동성 구간에서의 최대 레버리지 비율 : 200% (주식-파생형 펀드 기준 파생 최대 편입비 가정)
• 이외의 구간 : 시장 수익률

 

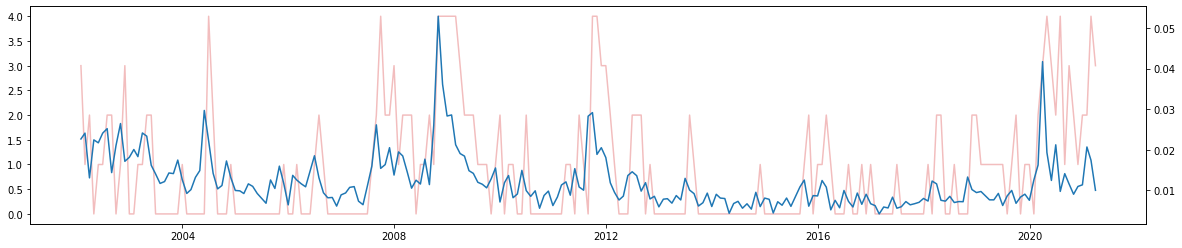
1) 기간별 레버리지 비율 추이

2) 성과 추이

3) 코멘트

• 박스권 구간에서 변동성이 낮게 나타나다보니 상대적으로 높은 레버리지 비율 사용
  → 레버리지 펀드의 효과가 나타남
  → 복리 효과로 인해 시장 대비 성과는 오히려 낮게 나타남 (아래 레버리지의 복리 효과 참고)

레버리지의 복리 효과

그런데 복리효과가 항상 좋은 것만은 아니다. 지수가 오르락내리락하는 변동장에선 복리효과가 오히려 독이 된다. 지수가 하루는 10% 상승하고, 다음날 10% 하락해 100-110-99가 되었다고 가정하면, 레버리지 ETF는 100-120-96이 된다. 누적수익률을 비교해 보면 지수는 -1%인 반면 레버리지 ETF는 -4%가 되는 것이다.
출처 : 매일경제.  https://www.mk.co.kr/news/economy/view/2011/09/570751

 

• 예상했던 대로 급락 구간에서 변동성 상승 
  → 편입비가 축소된 상태라 급락 이후 급반등하는 시장을 따라잡지 못하게 됨
  
  코로나 이후 단 1개의 최대 일간 수익률 데이터만 제외해도 시장과의 격차가 생각보다 크게 나타남
  

  

• 10년 가까이 이어진 박스피 & 코로나 대응능력 부재가 해당 전략 실패의 주요 요인으로 파악됨

 

V. 향후 과제

• 변동성 예측에 일중 데이터를 활용
  
  예를 들어, 하루 동안의 분봉 데이터의 움직임으로 그 날의 변동성을 측정하고 그 하루 하루의 변동성이 전체 기간에서는 일종의 클러스터를 형성할 것이라 가정하여, 일중 변동성이 크게 나타난 날은 다음날 포지션을 그만큼 작게 가져가는 전략은 어떨지?

 

VI. 주요 코드

 

max_leverage = 2.0
min_leverage = 0.6
rolling_size = 20

mkt_return = mkt['IKS200'].pct_change().dropna()
recent_std = mkt_return.rolling(rolling_size).std()

vmp_return = []
lev_rate = []
for base_num in range(rolling_size + 30, len(mkt_return)):
    
    # 최근 N일 변동성 계산
    base_date = mkt_return.index[base_num]
    as_is = recent_std[:base_num]

    # 오늘의 수익률
    return_t = mkt_return.loc[base_date]
    
    expected_vol = as_is[-1]  # 어제 예측한 오늘의 변동성
    target_vol = mkt_return.iloc[:base_num].std()  # 목표변동성 : 어제까지 전 기간 변동성
    expected_quintile = pd.qcut(as_is.values, q = 5, labels = False)[-1]  # 어제 예측한 오늘의 변동성 분위수

    if expected_quintile == 0:  # Scaled return (저변동성 구간)
        leverage_factor = np.min([target_vol / expected_vol, max_leverage])

    elif expected_quintile == 4:  # Scaled return (고변동성 구간)
        # print(expected_vol)
        leverage_factor = np.max([target_vol / expected_vol, min_leverage])

    else:  # Unscaled return 
        leverage_factor = 1

    scaled_return = return_t * leverage_factor

    vmp_return.append(scaled_return)
    lev_rate.append(leverage_factor)

vmp_return = pd.Series(vmp_return, index = mkt_return[rolling_size + 30:].index)
lev_rate = pd.Series(lev_rate, index = mkt_return[rolling_size + 30:].index)